Análisis INSAR
Utilizamos observaciones de radar de apertura sintética recopiladas por la misión Sentinel-1 A/B de la Agencia Espacial Europea.25 En el camino ascendente 78 cuadro 104 y en el camino descendente 85 cuadro 484 desde octubre de 2016 hasta abril de 2019 (Figura 1). Se crearon modelos de elevación digitales para parches de terreno utilizando datos de elevación de la Misión Topográfica de Radar Shuttle (SRTM-1) de la NASA con una resolución de 30 metros.26. Utilizando el software de procesamiento InSAR de código abierto GMTSAR27 Para crear interferogramas de dos pases, establecimos una línea de base temporal de 800 días y una línea de base vertical de 200 m para seleccionar pares interferométricos (Tabla S1). La región árida y escasamente vegetada del sureste de Nuevo México mantiene niveles de coherencia más altos en líneas de base temporales más largas que las regiones con mayor vegetación y/o nevadas, lo que nos permite crear pares de varios años que a menudo son altamente coherentes.
Todos los interferogramas se generan con la misma adquisición de referencia (17 de diciembre de 2016 para el camino ascendente; 11 de diciembre de 2016 para el camino descendente) y muchos de ellos muestran una alta coherencia y un ruido atmosférico mínimo de longitud de onda corta (Figura S1). Debido a la baja variabilidad observada en el ruido atmosférico en la escala subkilómetro que consideramos, no utilizamos correcciones atmosféricas del modelo. A partir de los interferogramas altamente coherentes, generamos una serie temporal con una referencia fija. Para detectar observaciones de interferencias en radianes de módulo 2π en cambios de línea de visión (LOS), utilizamos el algoritmo de costo estadístico y el algoritmo de cancelación de fase de red (SNAPHU).28. Luego recortamos las imágenes de fase a una escala local y eliminamos la función de pendiente bilineal que mejor se ajusta para reducir el ruido de fondo de longitud de onda larga, como los efectos de la troposfera y la ionosfera.29. Para comparar las observaciones de InSAR con los resultados del modelado geomecánico, analizamos conjuntos de datos de arriba hacia abajo y de abajo hacia arriba que abarcan períodos de tiempo similares en campos de deformación casi verticales y cercanos al este.30.
Aguas subterráneas y modelado geomecánico.
Seguimos los métodos descritos por Wangen et al.31 Para crear un modelo analítico 2D de las condiciones de inyección y litología de la roca en el sitio del pozo del Instituto Americano del Petróleo (API) No. 3002524312. Modelado de presión del yacimiento utilizando una solución transitoria 2D de la ecuación de flujo de agua subterránea para una formación isotrópica y homogénea, no establecemos -límites de flujo en la parte superior e inferior del acuífero, un campo infinito a la derecha y un límite de presión fijo en el lado izquierdo (ubicación del pozo). Asumimos una aproximación de deformación plana para modelar la geomecánica y relacionamos las ecuaciones mediante poroelasticidad estándar a través del módulo de Biot para relacionar la tensión efectiva y la sobreesfuerzo entre sí. Suponemos que la formación se deforma elásticamente mucho más rápido de lo que se propaga la onda de presión, lo que permite el acoplamiento unidireccional de la ecuación del flujo de agua subterránea a la solución de deformación de deformación plana.
Esta solución de presión plana, derivada de la descomposición de Fourier de la sobrepresión del tanque, determina la altura de la superficie sobre un tanque presurizado y una capa adicional de sobrecarga. Este sencillo modelo de dos capas tiene un tanque grueso, h1Y el espesor es pesado h2. El dominio lateral se extiende desde –a a a. Las condiciones límite incluyen que no haya desplazamiento vertical en la base del tanque, que la superficie sobrecargada esté sujeta a una presión normal nula y que la distribución de la presión, p (kh)es simétrico con respecto al eje z del pozo en x = 0 y llega a cero antes de que el campo termine en |x|= L.
Siguiendo a Wangen et al.31Determinamos la altura de la superficie, \(w\)en la ubicación x y el tiempo t de los términos compactos de la serie de Fourier para una presión inicial dada, s0Usando la ecuación. (1):
$$w\left( {x,t} \right) = \frac{{\alpha h_{1} p_{u} \left( {x,t} \right)}}{{\left( {\Lambda ) + 2G} \derecha)}}$$
(1)
dónde \(\alfa\) es el parámetro de Biot, Λ es el parámetro de Lameé y gramo Es el módulo de corte. Debido a que la distribución de presión \(p_{u} \left( {x,t} \right)\) de la inyección es una función par y se puede representar mediante la serie de Fourier de la función coseno:
$$p_{u} \left( {x,t} \right) = \frac{{a_{0} }}{2} + \mathop \sum \limits_{n = 1}^{\infty } f\ left( {k_{n} h_{1} ,k_{n} h_{2} } \right)a_{n} cos\left( {k_{n} x} \right).$$
(2)
donde esta el trabajo Fun valor adimensional entre 0 y 1, que representa la amplitud en la superficie que depende del número de onda, \(K\)y pescado h1 Y h2 Escrito como
$$f\left( {kh_{1} ,kh_{2} } \right) = \frac{1}{{kh_{1} }}\left( {cosh\left( {kh_{2} } \right )tanh\left( {kh_{1} + kh_{2} } \right) – sinh\left( {kh_{2} } \right)} \right).$$
(3)
Encontramos los coeficientes de Fourier, anorte, para distribuir la presión integrando la ecuación. (4)
$$a_{n} = \frac{2}{L}\mathop \smallint \limits_{0}^{L} p\left( {x,t} \right)cos\left( {n\pi x/ L} \right)dx,n = 0,1,2,…$$
(4)
dónde p(x,t) Representa sobrepresión en el momento adecuado. R La posición x recibe la presión inicial del fluido. s0 y difusión hidráulica Dr. Suponiendo una difusión hidráulica uniforme y resolviendo la ecuación de conservación del agua subterránea en 2D, aproximamos la propagación de la onda de presión usando.
$$\begin{array}{*{20}c} {p\left( {x,t} \right) = p_{0} erfc ({\frac{x}{{2\sqrt {Dt} }} }}) \\ \end{matriz},$$
(5)
Donde la erfc o función de error complementaria denota el área bajo los bordes de la función de densidad de probabilidad gaussiana32.
Modelamos dos condiciones separadas del sitio del pozo para tener en cuenta el historial del pozo de acuerdo con la División de Conservación de Petróleo de Nuevo México (NM-OCD), que proporciona detalles de las condiciones de operación, inyección/producción y mantenimiento en sitios de pozos individuales, incluidos aquellos dentro del vacío del campo de pozos. Por sus informes sabemos que Texaco comenzó a perforar el pozo API No. 3002524312 en diciembre de 1972, alcanzando una profundidad total de 1,463 metros antes de que comenzara la producción en enero de 1973.33. El pozo pasó de producción de petróleo a inyección de agua a principios de la década de 1980. Un estudio de inyección informado el 14 de agosto de 2017 provocó el cierre del pozo después de que se identificara una fuga en la carcasa de entre 256 y 265 metros. Todos los intentos de reparar el pozo fracasaron y después de que se encontró nuevamente en el pozo material de los estratos rojos que rodean la Formación del Lago Dewey, el pozo se tapó y, el 1 de septiembre de 2017, el sitio fue abandonado. Para resolver la fuente de la distorsión, creamos un modelo para la inyección profunda prevista en la Formación San Andrés a una profundidad de 1463 m, y otro para la inyección superficial que ocurre en el pozo entre 256 y 265 m.
Las formaciones Grayburg y San Andrés de la edad de Guadalupe constituyen el principal reservorio de carbonato del campo de pozos de vacío. Fallas de alto ángulo y bajo desplazamiento dividen el yacimiento horizontalmente34. El yacimiento se compone principalmente de dolomita y también contiene secciones de anhidrita impermeable y limolitas dolomíticas delgadas de muy baja permeabilidad.34, lo que también puede provocar que el tanque se parta. Incluyen formaciones de dolomita y anhidrita cubiertas por capas secundarias de esquisto y arenisca. Las formaciones más jóvenes consisten principalmente en dolomita, anhidrita, arenisca y halita.34. La formación más joven es la Formación Dewey Lake del Pérmico Tardío, que consta de arenisca fina y limolita cementada con anhidrita.35. Caparazón36 Atribuye las características geomorfológicas y sedimentológicas de la formación a la deposición en un sistema fluvial efímero caracterizado por inundaciones laminares y canales anchos y poco profundos de hasta dos metros de espesor que se apilan y se cruzan entre sí. Por encima de la Formación Dewey Lake se encuentra la Formación Santa Rosa del Triásico (Grupo Docum), un cuerpo complejo de arenisca con canales de hasta 30 m de espesor que se ha demostrado que es permeable en toda el área.37. Otros cuerpos de arena en el Grupo Dockum también se encuentran sobre la Formación basal Santa Rosa.38 Se los describe anecdóticamente como “bolsas de agua”; Sin embargo, debido a la mala calidad del agua en esta zona, las llanuras de arena de la Formación del Lago Dewey están relativamente inexploradas.
Modelado inverso
Formulamos el modelo directo descrito anteriormente como un problema inverso para determinar los valores de los parámetros del modelo a partir de la deformación observada. Usamos el marco de reflexión VMOD.39 Que realiza inversiones bayesianas a través del método Markov Chain Monte Carlo (MCMC) para inferir distribuciones de densidad de probabilidad posterior para valores de parámetros libres del modelo: profundidad del yacimiento/espesor de sobrecarga, ancho del yacimiento, presión del pozo, difusión y módulo de Young. Comenzamos con distribuciones previas uniformes utilizando límites de parámetros que representan la geometría del pozo, la litología del yacimiento y el exceso de revestimiento durante la inyección profunda (Tabla 1). La distribución previa es uniforme para describir la incertidumbre en los valores de los parámetros, mientras que los valores anteriores dentro de los límites de los parámetros especificados se eligen como el primer conjunto de valores de parámetros a partir del cual determinamos primero la probabilidad de generar el pico observado.
Invertimos los perfiles de elevación casi verticales en pasos de tiempo para crear una distribución posterior única. La ubicación del perfil (A a A’; ver Resultados en la sección «InSAR») se eligió lejos de las partes de deformación asimétrica para cumplir con el supuesto de simetría del modelo (ver Resultados). En la inversión, utilizamos perfiles durante 210 días (t6, ver Figura 5) y especificamos una única presión de pozo aplicada durante todo el período de simulación.
La inversión utiliza 3.100.000 pasos con un período de preparación para los primeros 100.000 pasos que se ignora para eliminar sesgos debidos a la elección de valores de parámetros anteriores. Luego tomamos muestras cada 1000 pasos para evitar recolectar muestras fuertemente correlacionadas. Esto da como resultado 3000 muestras de distribución posterior que parametrizan las distribuciones de densidad de probabilidad posterior.
Para recrear las condiciones operativas previstas en el sitio del pozo, utilizamos un modelo de dos capas que consiste en un yacimiento presurizado de Grayburg/San Andrés y una capa pesada de roca principalmente carbonatada (Figura 2a). El campo lateral se extiende hasta 1000 metros. Para calcular la distribución de presión, utilizamos los primeros 100 coeficientes de Fourier. anorte. Valores razonables para el factor peyote (\(\alfa\) = 0,7) y el coeficiente de Poisson \(\nu\) = 0,2) y se transfiere desde \(\nu\) y el módulo de Young, h, Definir valores para \(\lambda\) Y gramo.
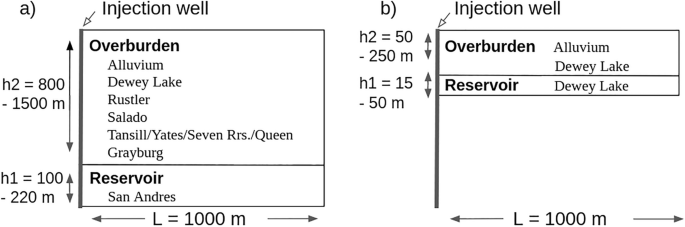
Los modelos de condiciones de los pozos de inyección se calcularon con un coeficiente de Biot de 0,7 y un índice de Poisson de 0,2. (a) Dibujo esquemático del modelo de inyección profunda: en este diseño, el fluido se inyecta alrededor del intervalo del pozo perforado. La cobertura consiste en formaciones superpuestas. (B) Diagrama esquemático del modelo de inyección superficial: el fluido se inyecta a una profundidad mucho menor en el pozo con menos carga.
Para determinar la magnitud del levantamiento en nuestro modelo de inyección superficial, utilizamos el método descrito anteriormente con los mismos supuestos básicos. Variamos los rangos de distribución previa uniforme (Tabla 1) para el modelo de inyección rompiendo el revestimiento del pozo poco profundo. La Formación Dewey Lake de lecho rojo se convierte en el reservorio compacto en la brecha y la cubierta superior está compuesta de areniscas, limolitas y limolitas (Figura 2b).

«Food ninja. Freelance pop culture fanatic. Wannabe zombie maven. Twitter aficionado.»







More Stories
Cómo los nuevos formatos fotónicos contribuyen al desarrollo de las tecnologías ópticas
La red social Butterflies AI añade una función que te convierte en un personaje de inteligencia artificial
Edición del vigésimo aniversario de Hautlence HLXX: redefiniendo el tiempo con minutos que retroceden y horas saltantes